Getting a feel for equivalence hypothesis testing
A few weeks ago, Daniel Lakens posted an excellent blog about equivalence hypothesis testing (http://daniellakens.blogspot.com/2016/05/absence-of-evidence-is-not-evidence-of.html). Equivalence hypothesis testing is a method to use frequentist statistical analyses (specifically, p-values) to provide support for a null hypothesis. Briefly, Lakens describes a form of equivalence hypothesis testing wherein the "null hypothesis" is a range of effects that are considered to be smaller than the smallest effect of interest. To provide evidence for a null effect a researcher performs 2 one-sided tests: One to determine if your effect is smaller than the upper boundary of the equivalence range and one to determine if your effect is larger than the lower boundary of the equivalence range. If your effect is both significantly less than the upper boundary and significantly greater than the lower boundary of the equivalence range, one can classify the effect as too small to be of interest. Of course, because these tests all employ the use of p-values, they are subject to a known long-run error rate (the familiar Type 1 and Type 2 errors). (If this brief description was too brief I would take the time to read Lakens' original blog post).
Although I could follow the logic of this equivalence testing procedure, I didn't have an "intuitive feel" for what it means to use p-values to generate support for a null effect. This is probably due to years of learning the traditional NHST approach to hypothesis testing wherein you can only "reject" or "fail to reject" the null hypothesis. Here is the process I went through to further my understanding of equivalence testing.
First, to get a feel for how p-values can be used to generate support for a null effect it is useful to get a feel for how p-values behave when there is an effect. Let's take a simple 2-group design where there is an effect of d = 0.3. Below is the distribution of p-values from 10,000 simulated studies with a population effect of d = 0.3 and with 50 individuals per group. You can see that 31.8% of these p-values are below .05. This figure is merely a visual representation of the statistical power of this design: Given a certain effect (e.g., d = 0.3), a certain sample size (e.g., N = 100), and an alpha level (e.g., .05), you will observe a p-value less than alpha at a known long-run rate. In this case, statistical power is 0.32.
Let's stick with the example where there is an effect of d = 0.3. Now suppose the sample size is doubled. In 10,000 simulated studies, increasing the sample size from 50 per group to 100 per group results in more low p-values. As can be seen below, 55.5% of the p-values are below .05. In other words, increasing the sample size increases statistical power. When there is a to-be-detected effect, increasing the sample size increases your chances of correctly detecting that effect by obtaining a p-value below .05. In this case, statistical power is 0.55.
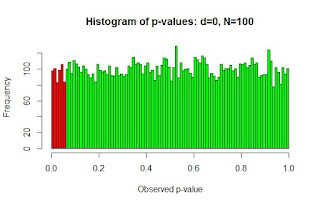
In comparison, let's look at a scenario where there is no effect in the population, d = 0 (which is the scenario that is most relevant to equivalence testing). With no effect in the population you can only make Type 1 errors. In 10,000 simulated studies where there is a population effect of zero (i.e., d = 0) and a total N of 100, 5.17% of the p-values were below .05. (If you ran this simulation again you might observe slightly more or slightly fewer p-values below .05. In the long run 5% of the studies will result in p-values below .05). The 5% of studies with low p-values are all Type 1 errors because there is no effect in the population.
Sticking with the scenario where we have a population effect of zero (i.e., d = 0) and we double the sample size from a total N of 100 to a total N of 200. The distribution of p-values from 10,000 simulated studies shows that 4.87% of the p-values were less than .05 (again, in the long run this will be exactly 5%). When there is no effect in the population the distribution of p-values does not change when the sample size changes.
To recap: When there is a to-be-detected effect you can only make Type 2 errors. With all else being equal, increasing the sample size increases statistical power which, by definition, decreases the likelihood of making a Type 2 error. When there is no effect you can only make Type 1 errors. With all else being equal, increasing the sample size does not affect the distribution of observed p-values. In other words, when a null effect is true, your statistical power will simply be your alpha level regardless of sample size.
What does this have to do with equivalence testing? A lot actually. If you followed the information above, then understanding equivalence testing is just re-arranging and re-framing this already-familiar information.
For the following simulations we are assuming there is no effect in the population (i.e., d = 0). We also are assuming that you determined that an absolute effect less than d = 0.4 is either too small for you to consider meaningful or it is too resource expensive for you to study. (This effect was chosen only for illustrative purposes, you can use whatever effect you want.)
To provide support for a null effect it is insufficient to merely fail to reject the null hypothesis (i.e., observe a p-value greater than your alpha level) because a non-significant effect can either indicate a null effect or a weakly powered test of a true effect that results in a Type 2 error. And, as shown above, increasing your sample size does not increase your chances of detecting a true null effect with traditional NHST. However, increasing your sample size can increase the statistical power to detect a null effect with equivalence testing.
Let's run some simulations. We have already seen that if a null effect is true (d = 0) and your total sample size is 100 that traditional NHST will result in 5% of p-values less than .05 in the long run. I now took these 10,000 simulated studies and I tested whether the effects were significantly smaller than d = 0.4 and whether the effects were significantly larger than d = -0.4. As can be seen below, in these 10,000 simulations, when d = 0 and N = 100, 63.9% of the samples resulted in an effect that was significantly smaller than d = 0.4 and 63.1% of samples resulted in an effect that was significantly larger than d = -0.4 (these percentages are not identical because of randomness in the simulation procedure; in the long run they will be equal).
Some of the samples with effects that are significantly smaller than d = 0.4 actually have effects that are much smaller than d = 0.4. These samples have effects that are significantly smaller than d = 0.4 but are not significantly larger than d = -0.4. Likewise, some of these samples with effects that are significantly larger than d = -0.4 have effects that are much larger than d = -0.4. These samples have effects that are significantly larger than d = -0.4 but are not significantly smaller than d = 0.4.
In equivalence testing, to classify an effect as "null" requires the effect to be both significantly less than the upper bound of the equivalence range and significantly higher than the lower bound of the equivalence range. In these 10,000 samples, 27.04% of the samples would be considered "null" (i.e., d = -0.4 < observed effect < d = 0.4).
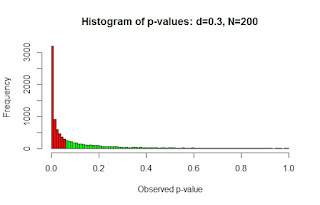
Now comes the real the utility of equivalence testing. If we double the total sample size from N = 100 to N = 200 we can increase the statistical power of claiming evidence for the null hypothesis. As can be seen below, within the 10,000 simulated studies where d = 0 and N = 200, 88.3% of the studies had effects that were significantly smaller than d = 0.4 and 88% had effects that were significantly greater than d = -0.4. (again, differences in these percentages are due to randomness in the data generation process and are not meaningful), and 76.4% of these studies had effects that were both smaller than d = 0.4 and greater than d = -0.4. Thus, increasing the total sample size from 100 to 200 increased the percentage of studies that would be classified as "null" (i.e., d = -0.4 < observed effect < d = 0.4) from 27.04% to 76.4%.
Here are the major take-home messages. First, equivalence testing is nice because it allows you to provide evidence for a null effect by using the tools that most researchers are already familiar with (i.e., p-values). Second, unlike traditional NHST, increasing N can increase the statistical power of detecting a null effect (defined by the equivalence range) when using equivalence testing.
These simulations are how I went about building my understanding of equivalence testing. I hope this helps others build their understanding too. The R-code for this post can be accessed here (https://osf.io/ey5wq/). Feel free to use this code for whatever purposes you want and please point out any errors you find.
Although I could follow the logic of this equivalence testing procedure, I didn't have an "intuitive feel" for what it means to use p-values to generate support for a null effect. This is probably due to years of learning the traditional NHST approach to hypothesis testing wherein you can only "reject" or "fail to reject" the null hypothesis. Here is the process I went through to further my understanding of equivalence testing.
In comparison, let's look at a scenario where there is no effect in the population, d = 0 (which is the scenario that is most relevant to equivalence testing). With no effect in the population you can only make Type 1 errors. In 10,000 simulated studies where there is a population effect of zero (i.e., d = 0) and a total N of 100, 5.17% of the p-values were below .05. (If you ran this simulation again you might observe slightly more or slightly fewer p-values below .05. In the long run 5% of the studies will result in p-values below .05). The 5% of studies with low p-values are all Type 1 errors because there is no effect in the population.
Sticking with the scenario where we have a population effect of zero (i.e., d = 0) and we double the sample size from a total N of 100 to a total N of 200. The distribution of p-values from 10,000 simulated studies shows that 4.87% of the p-values were less than .05 (again, in the long run this will be exactly 5%). When there is no effect in the population the distribution of p-values does not change when the sample size changes.
To recap: When there is a to-be-detected effect you can only make Type 2 errors. With all else being equal, increasing the sample size increases statistical power which, by definition, decreases the likelihood of making a Type 2 error. When there is no effect you can only make Type 1 errors. With all else being equal, increasing the sample size does not affect the distribution of observed p-values. In other words, when a null effect is true, your statistical power will simply be your alpha level regardless of sample size.
What does this have to do with equivalence testing? A lot actually. If you followed the information above, then understanding equivalence testing is just re-arranging and re-framing this already-familiar information.
For the following simulations we are assuming there is no effect in the population (i.e., d = 0). We also are assuming that you determined that an absolute effect less than d = 0.4 is either too small for you to consider meaningful or it is too resource expensive for you to study. (This effect was chosen only for illustrative purposes, you can use whatever effect you want.)
To provide support for a null effect it is insufficient to merely fail to reject the null hypothesis (i.e., observe a p-value greater than your alpha level) because a non-significant effect can either indicate a null effect or a weakly powered test of a true effect that results in a Type 2 error. And, as shown above, increasing your sample size does not increase your chances of detecting a true null effect with traditional NHST. However, increasing your sample size can increase the statistical power to detect a null effect with equivalence testing.
Let's run some simulations. We have already seen that if a null effect is true (d = 0) and your total sample size is 100 that traditional NHST will result in 5% of p-values less than .05 in the long run. I now took these 10,000 simulated studies and I tested whether the effects were significantly smaller than d = 0.4 and whether the effects were significantly larger than d = -0.4. As can be seen below, in these 10,000 simulations, when d = 0 and N = 100, 63.9% of the samples resulted in an effect that was significantly smaller than d = 0.4 and 63.1% of samples resulted in an effect that was significantly larger than d = -0.4 (these percentages are not identical because of randomness in the simulation procedure; in the long run they will be equal).
In equivalence testing, to classify an effect as "null" requires the effect to be both significantly less than the upper bound of the equivalence range and significantly higher than the lower bound of the equivalence range. In these 10,000 samples, 27.04% of the samples would be considered "null" (i.e., d = -0.4 < observed effect < d = 0.4).
Now comes the real the utility of equivalence testing. If we double the total sample size from N = 100 to N = 200 we can increase the statistical power of claiming evidence for the null hypothesis. As can be seen below, within the 10,000 simulated studies where d = 0 and N = 200, 88.3% of the studies had effects that were significantly smaller than d = 0.4 and 88% had effects that were significantly greater than d = -0.4. (again, differences in these percentages are due to randomness in the data generation process and are not meaningful), and 76.4% of these studies had effects that were both smaller than d = 0.4 and greater than d = -0.4. Thus, increasing the total sample size from 100 to 200 increased the percentage of studies that would be classified as "null" (i.e., d = -0.4 < observed effect < d = 0.4) from 27.04% to 76.4%.
These simulations are how I went about building my understanding of equivalence testing. I hope this helps others build their understanding too. The R-code for this post can be accessed here (https://osf.io/ey5wq/). Feel free to use this code for whatever purposes you want and please point out any errors you find.
Comments
Post a Comment